Quickstart¶
pyeee: A Python library for parameter screening of computational models using Morris’ method of
Elementary Effects or its extension of Efficient or Sequential Elementary Effects by Cuntz, Mai et
al. (Water Res Research, 2015).
About¶
pyeee is a Python library for performing parameter screening of computational models. It uses
Morris’ method of Elementary Effects and also its extension of Efficient or Sequential Elementary
Effects published by:
Cuntz M, Mai J et al. (2015) Computationally inexpensive identification of noninformative model parameters by sequential screening Water Resources Research 51, 6417-6441, doi:10.1002/2015WR016907.
pyeee can be used with Python functions and external programs, using for example the package
partialwrap. Function evaluation can be distributed with Python’s multiprocessing or via
MPI.
The complete documentation for pyeee is available from Read The Docs.
Quick usage guide¶
Simple Python function¶
Consider the Ishigami-Homma function: 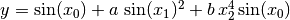 .
.
Taking 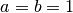 gives:
gives:
import numpy as np
def ishigami1(x):
return np.sin(x[0]) + np.sin(x[1])**2 + x[2]**4 * np.sin(x[0])
The three parameters 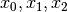 follow uniform distributions between
follow uniform distributions between 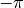 and
and
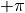 .
.
Morris’ Elementary Effects can then be calculated like:
npars = 3
# lower boundaries
lb = np.ones(npars) * (-np.pi)
# upper boundaries
ub = np.ones(npars) * np.pi
# Elementary Effects
from pyjams import ee
np.random.seed(seed=1023) # for reproducibility of examples
out = ee(ishigami1, lb, ub, 10)
which gives the Elementary Effects (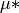 ):
):
# mu*
print("{:.1f} {:.1f} {:.1f}".format(*out[:,0]))
# gives: 173.1 0.6 61.7
Sequential Elementary Effects distinguish between informative and uninformative parameters using several times Morris’ Elementary Effects:
# screen
from pyeee import eee
np.random.seed(seed=1021) # for reproducibility of examples
out = eee(ishigami1, lb, ub)
which returns a logical ndarray with True for the informative parameters and False for the uninformative parameters:
print(out)
# gives: [ True False True]
Python function with extra parameters¶
The function for pyeee must be of the form func(x). Use Python’s functools.partial()
from the functools module to pass other function parameters.
For example pass the parameters  and
and 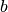 to the Ishigami-Homma function:
to the Ishigami-Homma function:
from functools import partial
def ishigami(x, a, b):
return np.sin(x[0]) + a * np.sin(x[1])**2 + b * x[2]**4 * np.sin(x[0])
def call_func_ab(func, a, b, x):
return func(x, a, b)
# Partialise function with fixed parameters a and b
a = 0.5
b = 2.0
func = partial(call_func_ab, ishigami, a, b)
npars = 3
# lower boundaries
lb = np.ones(npars) * (-np.pi)
# upper boundaries
ub = np.ones(npars) * np.pi
# Elementary Effects
np.random.seed(seed=1021) # for reproducibility of examples
out = ee(func, lb, ub, 10)
Figuratively speaking, partial passes  and
and 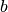 to the function call_func_ab
already during definition so that
to the function call_func_ab
already during definition so that pyeee can then simply call it as func(x), so that x is
passed to call_func_ab as well.
Function wrappers¶
We recommend to use the package partialwrap, which provides wrappers to use with partial.
from partialwrap import function_wrapper
args = [a, b]
kwargs = {}
func = partial(function_wrapper, ishigami, args, kwargs)
# screen
np.random.seed(seed=1021) # for reproducibility of examples
out = eee(func, lb, ub)
There are wrappers to use with Python functions with or without masking parameters, as well as wrappers for external programs.
Installation¶
The easiest way to install is via pip:
pip install pyeee
See the installation instructions for more information.
License¶
pyeee is distributed under the MIT License.
See the LICENSE file for details.
Copyright (c) 2013-2021 Matthias Cuntz, Juliane Mai
The project structure is based on a template provided by Sebastian Müller .
Contributing to pyeee¶
Users are welcome to submit bug reports, feature requests, and code contributions to this project through GitHub.
More information is available in the Contributing guidelines.